Could you write and then read an entire 3TB drive five times without an error?
Suppose you were to run a burn in test on a brand new Seagate 3TB SATA drive, writing 3TB and then reading it back to confirm the data. Our standards are such that if a drive fails during 5 cycles we won’t ship it. Luckily, all 20 of 20 drives we tested last night passed. In fact, most of the 3TB drives we test every week passed this test. Why is that a big deal? Because there is a calculation floating around out there that shows when reading a full 3TB drive there is a 21.3% chance of getting an unrecoverable read error. Clearly the commonly used probability equation isn’t modeling reality. To me this raises red flags on previous work discussing the viability of both stand alone SATA drives and large RAID arrays.
It’s been five years since Robin Harris pointed out that the sheer size of RAID-5 volumes, combined with the manufacturer’s Bit Error Rate (how often an unrecoverable read error occurs reading a drive) made it more and more likely that you would encounter an error while trying to rebuild a large (12TB) RAID-5 array after a drive failure. Robin followed up his excellent article with another “Why RAID-6 stops working in 2019” based on work by Leventhal. Since RAID-5 is still around it seems Mark Twain’s quote “The reports of my death are greatly exaggerated” is appropriate.
Why hasn’t it happened? Certainly RAID-6 has become more popular in server storage systems. But RAID-5 is still used extensively, and on 12TB and larger volumes that Robin predicts don’t recover well from drive failures. Before I get into some mind numbing math let me give away what I think might be an answer: Because the Bit Error Rate (BER) for some large SATA drives are clearly better than what the manufacturer says. The spec is expressed as a worst case scenario and in the real world experience is different.
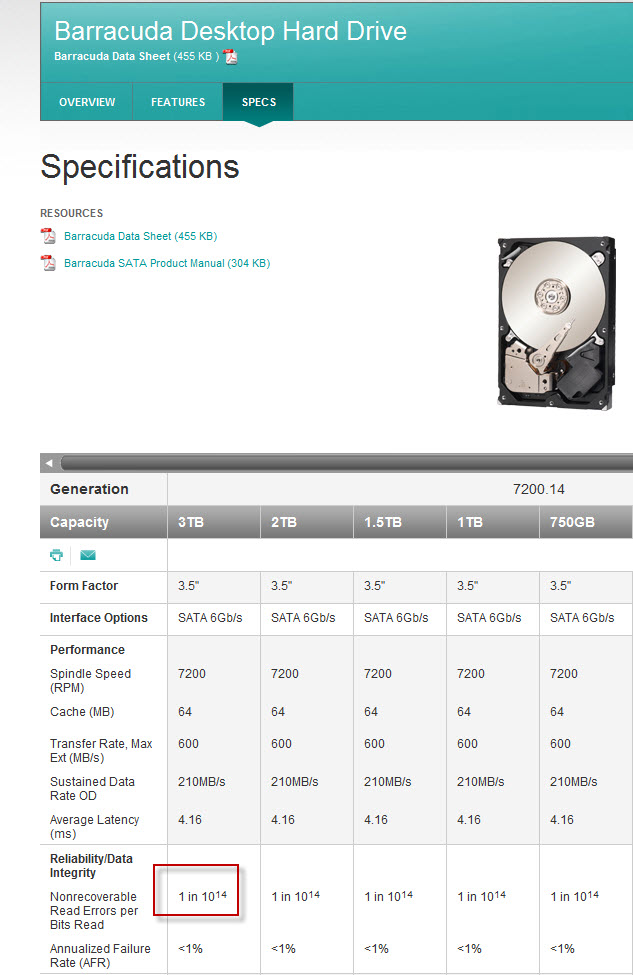 Seagate’s BER on 3TB drives is stated as 10^14, but may be understated. Hitachi’s bit error rate on their 4TB SATA drives are 10^15 and in my experience the two drives perform similarly from a reliability perspective. That order of magnitude makes a big difference on the calculations of expected read errors. Let me set the stage by going back over the probability equation used by Robin Harris and Adam Leventhal.
Seagate’s BER on 3TB drives is stated as 10^14, but may be understated. Hitachi’s bit error rate on their 4TB SATA drives are 10^15 and in my experience the two drives perform similarly from a reliability perspective. That order of magnitude makes a big difference on the calculations of expected read errors. Let me set the stage by going back over the probability equation used by Robin Harris and Adam Leventhal.
The probability equation they use for a successful read of all bits on a drive is
(1-1/b)a
“b” = the Bit Error Rate (BER) also known as Unrecoverable Read Error(URE) rate
“a” = Number of Bits read (the amount of data on an entire volume or drive)
We can use sectors, bytes or bits for this calculation as long as we stay consistent. In this article Leventhol uses sectors, which I think just complicates the calculation but let’s confirm his numbers. He calculates that a 100GB disk array has 200 million 512byte sectors. So a=2.0×10^8. He uses b= 24 Billion (2.4×10^10) because he says the bit error rate is 10^14 which you divide by 512bytes per sector and 8bits per bite. He determines the chance of array failure during a rebuild is only 0.8 percent. From his article: (1 — 1/(2.4 x 1010)) ^ (2.0 x 108) = 99.2%. This means that on average, 0.8 percent of disk failures would result in data loss due to an uncorrectable bit error.”
Now we can confirm whether we get the same results by typing the values into our formula on http://web2.0calc.com/. I wanted to flip this equation from probability of success to calculate the probability of a failure directly and then express it as a percentage so I just subtract the success rate from 1 and multiply times 100:
100(1-(1-1/b)a )
Cut and paste the string below into the website calculator and hit the equal key:
100*(1-(1-1/(2.4E10))^(2E8)) = 0.83% (I’ve rounded off)
This is the same number the author got, indicating less than 1% chance of failure while reading an entire 100GB array or volume.
Personally I think it is easier to do all this by leaving all the numbers in bits. This is because the hard drive vendors express “b” or “BER” in bits rather than sectors. For example, this Seagate data sheet shows for Barracuda SATA drives the number for “Nonrecoverable Read Errors per Bits read, Max” is 1014 This is the same number the author used above. We express this in scientific notation for the variable “b” as 1E14 (1 times 10 to the 14th). This is about 12.5TeraBytes. The value for “a” on a 100GB volume can be written as 100 followed by 9 zeros. We must multiply by 8 bits per byte to get the number of bits.
Probability of a read error while reading all of a 100GB volume using SATA drives
100*(1-(1-1/(1E14))^(100E9*8)) = 0.80% (rounded off)
So we’re getting about the same answer using bits instead of sectors (subject to some rounding errors) and I think using bits is a little less confusing don’t you?
Robin Harris did the calculation on a 12TB array and got a whopping 62% chance of data loss during a RAID rebuild. Can we confirm his math using bits instead of sectors and the same formula? As before copy and paste this into web2.0calc.com:
100*(1-(1-1/(1E14))^(12000E9*8)) = 61.68% Yep. At least our math is tracking. Now that we’re getting the same results as the experts we’re ready to try our own calculations using real world hard drives. Let’s not even talk about RAID. Let’s just take a stand alone Seagate 3TB drive and see what is the probability we’ll get a single non-recoverable read error if we fill and read the whole drive.
Probability of a read error while reading all of a Seagate 3TB SATA drive
100*(1-(1-1/(1E14))^(3000E9*8)) = 21.3% (rounded off)
So after all this math I get the number I started this article with – a 21.3% chance of a single read failure. But wait a minute!!! Does that sound right to you? Doesn’t that mean that if I fill a 3TB drive and read all the bits about 5 times that I will likely encounter an error that the drive can’t recover from? If that were true it would mean 3TB drives would be unusable! Just for grins lets try a Hitachi 4TB drive with it’s slightly better BER of 10^15:
Probability of a failure while reading all of a 4TB Hitachi SATA drive 
100*(1-(1-1/(1E15))^(4000E9*8)) =3.14% (Honest-I didn’t try to get Pi)
Well that’s better! But if my 4TB drive is going to fail 3% of the time when I read the whole thing I’m still pretty concerned.
Summary
I previously pointed out that our burn-in test alone disproves the calculated failure rates. We use these drives (both 3TB and 4TB) a lot in a mirroring backup system where drives are swapped nightly and re-mirrored. Since the mirroring is done at the block level the entire drive is ALWAYS read to create a new copy with its mirror partner. Which means, we should see some of these read errors on a regular basis. In fact, our media often goes for years without a problem.
Similarly, our failure rates rebuilding large 8TB RAIDPacs are nowhere near what this probability formula suggests (6%). So should we believe real world results or the math? Maybe a hard drive expert can suggest why the formula isn’t properly modeling the real world. I’m not the only one to notice that the probability formula doesn’t map to real world results: http://www.raidtips.com/raid5-ure.aspx
There is no question that both probability of read error during rebuilds, along with some of the other concerns about large arrays taking a while to rebuild due to limitations of the interface and drive speed should play into future planning and product design. Right now our RAID-5 three-drive RAIDPacs are rebuilding at about 250-300 Gigabytes per hour, so an 8TB RAIDPac can take about 26 hours to rebuild. Luckily, we use RAID for backup media rather than primary storage so speed of rebuild isn’t as large an issue for our clients. Drive failures are relatively infrequent (about 3 drive failures out of 100 per year) and multiple RAIDpac backup appliances are used to duplicate data. Even when we raise the size of our RAIDPac to 12TB using three 6TB drives the issues will be manageable, though rebuild time will go to 1.67 days. We’ll continue to watch this issue and continue to make backup reliable, but for now it’s safe to say RAID-5 is alive and well.
2015 UPDATE: Using RAID-5 Means the Sky is Falling!

